Where Am I? Estimating Location In Runescape With The Mini-Map
# see appendix for more info
%run blog/utilities.ipynb
Solving Runescape So I Can Finally Quit
Runescape is a boring video game for losers. In the game, your location is represented to you in both a world map and a mini-map. My goal was to estimate the player’s location on the world map using only the mini-map. Real-time location estimation is the first step in breaking the game so that it can play itself and we can all go home.
world_map_lumbridge = load_image('/images/rotation_estimation/world_map_lumbridge.png')
north_oriented_map = load_image('/images/rotation_estimation/north_oriented_map.png')
fig, axes = plt.subplots(1,2, dpi=200)
axes[0].imshow(north_oriented_map)
axes[0].set_title('The player\'s minimap')
axes[1].imshow(world_map_lumbridge)
axes[1].set_title('A small piece of the world map')
fig.subplots_adjust(wspace=.5)

If The Mini-Map Is Oriented North
So we’re given an image of the mini-map, and we estimate the corresponding location on the world map. If the mini-map is north-facing, this is a fairly simple problem. We can simply take the map from the mini-map and template search to find it on the world map.
cropped_mini_map = load_image('/images/rotation_estimation/cropped_mini_map.png', scale=1.5)
# template search
method = cv.TM_CCOEFF_NORMED
res = cv.matchTemplate(cropped_mini_map, world_map_lumbridge, method)
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res, None)
# plot the estimated match
template_match_plotted = world_map_lumbridge.copy()
cv.rectangle(template_match_plotted,
(max_loc[0], max_loc[1]),
(max_loc[0] + cropped_mini_map.shape[0], max_loc[1] + cropped_mini_map.shape[1]),
(255, 0, 0), 3, 8, 0)
show_images(cropped_mini_map, template_match_plotted, 'The cropped mini-map', 'The corresponding template match (Good)')

If The Mini-Map Is Not Oriented North
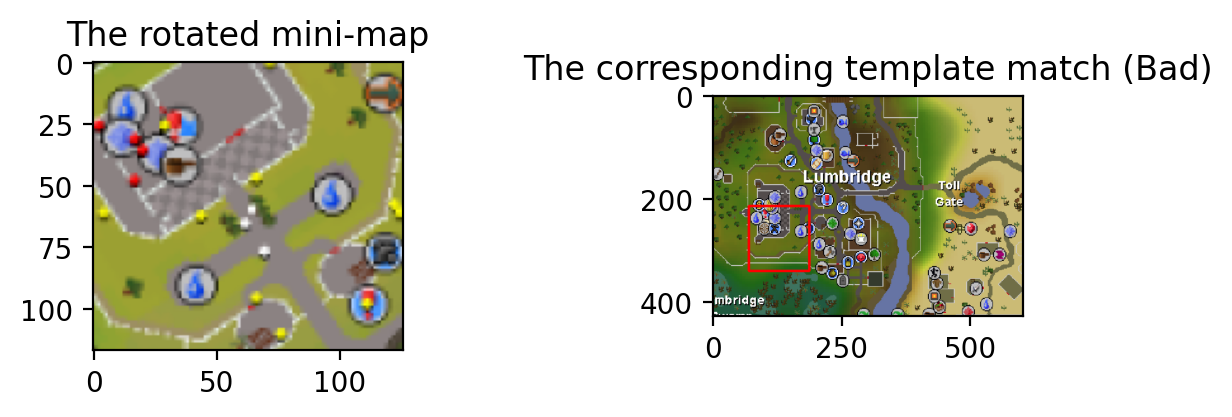
In this case, we can’t apply a template search right away. The map is crooked, so we won’t get good detections
crooked_mini_map = load_image('/images/rotation_estimation/crooked_mini_map.png', scale=1.5)
# template search
method = cv.TM_CCOEFF_NORMED
res = cv.matchTemplate(crooked_mini_map, world_map_lumbridge, method)
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res, None)
# plot the estimated match
result_plotted = world_map_lumbridge.copy()
cv.rectangle(result_plotted,
(max_loc[0], max_loc[1]),
(max_loc[0] + crooked_mini_map.shape[0], max_loc[1] + crooked_mini_map.shape[1]),
(255, 0, 0), 3, 8, 0)
show_images(crooked_mini_map, result_plotted, 'The rotated mini-map', 'The corresponding template match (Bad)')
So, how could we convert a rotated mini-map back into a north-facing minimap?
north_east_oriented_map = load_image('/images/rotation_estimation/north_east_oriented_map.png')
show_images(north_east_oriented_map, north_oriented_map, 'The map we are given', 'The map we want to convert to')

Extracting Angle Information From The Compass By Transforming Between Features
If we can determine the angle of rotation, then we can rotate the mini-map image to match its north-facing counterpart. We can estimate the angle of rotation using the compass. The first step is to detect “features” on the rotated compass and correspond them to features on the north-facing compass. First we detect features using the SIFT algorithm.
compass_north = load_image('/images/rotation_estimation/compass_north.png', scale=2.5, color=cv.COLOR_BGR2GRAY)
compass_north_east = load_image('/images/rotation_estimation/compass_northeast.png', scale=2.5, color=cv.COLOR_BGR2GRAY)
# Initiate SIFT detector
sift = cv.SIFT_create()
# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(compass_north_east, None)
kp2, des2 = sift.detectAndCompute(compass_north, None)
compass_north_east_features = compass_north_east.copy()
compass_north_features = compass_north.copy()
compass_north_east_features = cv.drawKeypoints(compass_north_east, kp1, compass_north_east_features, flags=cv.DRAW_MATCHES_FLAGS_DEFAULT)
compass_north_features = cv.drawKeypoints(compass_north, kp2, compass_north_features, flags=cv.DRAW_MATCHES_FLAGS_DEFAULT)
show_images(compass_north_features, compass_north_east_features, 'Features for north compass', 'Features for north-east compass')

Next we pair the features between the compasses using Flann matcher, which takes advantage of the gradient information represented in SIFT features. We won’t go into details on how this works. We use Flann to get acceptable matches according to some threshold
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2)
lowe_ratio_threshold = 0.7
good_matches = []
for m, n in matches:
if m.distance < lowe_ratio_threshold * n.distance:
good_matches.append(m)
img_matches = np.empty(
(max(compass_north_east.shape[0], compass_north.shape[0]), compass_north_east.shape[1]+compass_north.shape[1], 3), dtype=np.uint8)
cv.drawMatches(compass_north_east, kp1, compass_north, kp2,
good_matches, img_matches, flags=cv.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS)
plt.imshow(img_matches)
<matplotlib.image.AxesImage at 0x7fc6f4a09d30>
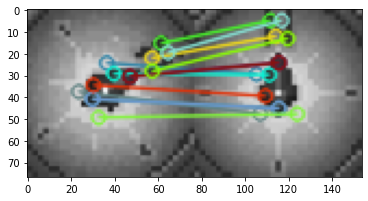
Now we want to calculate an explicit translation between the paired features of the two compasses. We can do this if we make an assumption that the compasses are related by an affine function, i.e. a mix of scaling, rotation, and translation. In reality, we should find out that the transformation is almost entirely rotation with very little scaling.
A 2D affine transformation involving a scaling by $s_x, s_y$, shearing by $c_x, c_y$, rotation by $\theta$, and a translation by $x_t, y_t$, can be represented in 3D as a linear transformation with the help of homogenous coordinates,
\[M = \left[ {\begin{array}{cc} s_x\cos{\theta} & -c_x\sin{\theta} & x\\ c_y\sin{\theta} & s_y\cos{\theta} & y\\ 0 & 0 & 1\\ \end{array} } \right]\]So that we can map a feature at $(x,y)$ on the original image to the corresponding feature at $(x’, y’)$ on the final image
\[M \left[ {\begin{array}{cc} x\\ y\\ 1\\ \end{array} } \right] = \left[ {\begin{array}{cc} x'\\ y'\\ 1'\\ \end{array} } \right]\]We will approximate the best of these matrices for mapping between the features of the two compasses using OpenCV’s EstimateAffine2D. Then we can simply calculate $\theta$ from the matrix we obtain.
EstimateAffine2D uses Random Sample Consensus, or RANSAC, to estimate the affine transformation from our limited set of sample points.
##
src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
M, mask = cv.estimateAffine2D(src_pts, dst_pts, cv.RANSAC)
M
array([[ 0.57565154, 0.85025771, -14.11907287],
[ -0.8060638 , 0.58425459, 44.51285597]])
Wow, very cool. Let’s assume that $c_x, s_x \approxeq 1$. Then we can calculate our angle of rotation as $\arctan{(\sin{\theta},\cos{\theta})}=\arctan{(-M_{01}, M_{00})}$
angle = np.arctan2(-1 * M[0, 1], M[0, 0])
angle
-0.9756521224680054
This is about $.3\pi$ radians. Let’s get convert that to English.
angle_degrees = angle * (180.0/np.pi)
angle_degrees
-55.90074889039763
Very nice. Looks like we’ve got our angle, boys. I’m a little worried about the simplifying assumptions we made (i.e. that $c_x, s_x \approxeq 1$), but I’ve found that in practice this does a pretty darn good job of consistently approximating the angle. It also doesn’t matter, since our mini-map correction will use the whole translation matrix.
Rotating The Mini-Map
Okay, let’s bring it home now. We need to use the calculated transformation to rotate our mini-map so that it is once again north-facing. Let’s try it with our compass first.
rows, cols = compass_north_east.shape[:2]
corrected_compass = cv.warpAffine(compass_north_east, M, (cols, rows))
show_images(compass_north_east, corrected_compass, 'The compass we were given', 'The corrected compass we computed', cmap='gray')

Great, now let’s try the mini-map
crooked_mini_map = load_image('/images/rotation_estimation/crooked_mini_map.png')
corrected_mini_map = cv.warpAffine(crooked_mini_map, M, (cols, rows))
show_images(crooked_mini_map, corrected_mini_map, 'The mini-map we were given', 'The corrected mini-map we computed')

I resized to make sure the mini-map is actually the same size as the compass we used to calculate the transformation. This makes the procedure more reliable in the face of weird translation shenanigans.
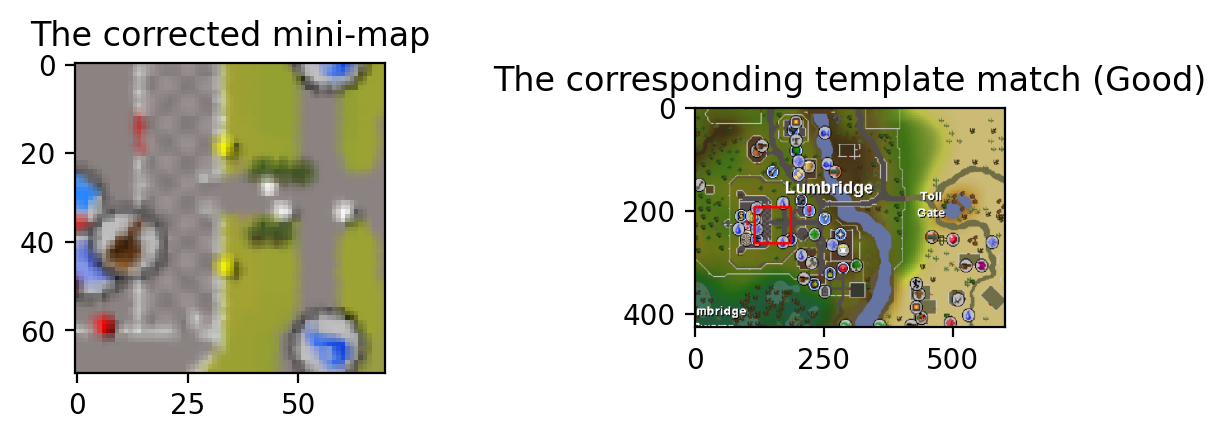
Finally, we can resize to the proper scale for a template search, trim off the gross bits on the corners, and figure out where in the world we are
rows, cols = corrected_mini_map.shape[:2]
trim = int((np.sqrt(rows*rows + cols*cols) - rows)//2)
final_mini_map = corrected_mini_map[trim:(-1*trim), trim:(-1*trim)]
final_mini_map = scale_img(final_mini_map, 1.5)
# template search
method = cv.TM_CCOEFF_NORMED
res = cv.matchTemplate(final_mini_map, world_map_lumbridge, method)
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res, None)
# plot the estimated match
template_match_plotted = world_map_lumbridge.copy()
cv.rectangle(template_match_plotted,
(max_loc[0], max_loc[1]),
(max_loc[0] + final_mini_map.shape[0], max_loc[1] + final_mini_map.shape[1]),
(255, 0, 0), 3, 8, 0)
show_images(final_mini_map, template_match_plotted, 'The corrected mini-map', 'The corresponding template match (Good)')
Conclusion
Runescape is a horrible game. All you do is grind repetitive tasks to gain experience and gold pieces. Anyone could play it. Why can’t a computer? I’m trying to design a representation of the game that makes it playable by a computer in a human-like way. To do this, I’m breaking the game into conceptual components that I can model mathematically. For example, here we have established that the player is a point on a two-dimensional surface, and that the coordinates of both the player and world locations can be established using computer vision along with a copy of the world map.
The next thing I will be exploring is using object detection to detect interactable components of the screen, such as “seeing” that there is a goblin which I can attack. I’ll also be working on the Ratcatchers quest in OSRS because my stupid computer can’t do it for me.
Appendix
blog/utilities.ipynb
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
import os
def scale_img(img, scale_percent):
width = int(img.shape[1] * scale_percent)
height = int(img.shape[0] * scale_percent)
dim = (width, height)
return cv.resize(img, dim, interpolation=cv.INTER_AREA)
def load_image(img_dir, scale=None, color=cv.COLOR_BGR2RGB):
img = cv.imread(img_dir)
img = cv.cvtColor(img, color)
if scale is not None:
img = scale_img(img, scale)
return img
def show_images(img1, img2, title1, title2, wspace=1, dpi=200, cmap=None):
fig, axes = plt.subplots(1,2, dpi=dpi)
axes[0].imshow(img1, cmap=cmap)
axes[0].set_title(title1)
axes[1].imshow(img2, cmap=cmap)
axes[1].set_title(title2)
fig.subplots_adjust(wspace=wspace)
def make_grayscale_and_resize(img, scale):
new_img = cv.cvtColor(img, cv.COLOR_RGB2GRAYSCALE)
new_img = scale_img(new_img, scale)
return new_img